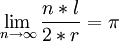Sistema hexadecimal




De Wikipedia, la enciclopedia libre
(Redirigido desde
Hexadecimal)
El sistema hexadecimal, a veces abreviado como hex, es el sistema de numeración posicional de base 16 —empleando por tanto 16 símbolos—. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa 28 valores posibles, y esto puede representarse como  , que, según el teorema general de la numeración posicional, equivale al número en base 16 10016, dos dígitos hexadecimales corresponden exactamente —permiten representar la misma línea de enteros— a un byte.
, que, según el teorema general de la numeración posicional, equivale al número en base 16 10016, dos dígitos hexadecimales corresponden exactamente —permiten representar la misma línea de enteros— a un byte.
En principio dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos sería, por tanto, el siguiente:

Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito es alterado dependiendo de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16. Por ejemplo: 3E0A16 = 3×162 + E×161 + 0×160 + A×16-1 = 3×256 + 14×16 + 0×1 + 10×0,0625 = 992,625.
El sistema hexadecimal actual fue introducido en el ámbito de la computación por primera vez por IBM en 1963. Una representación anterior, con 0–9 y u–z, fue usada en 1956 por la computadora Bendix G-15.
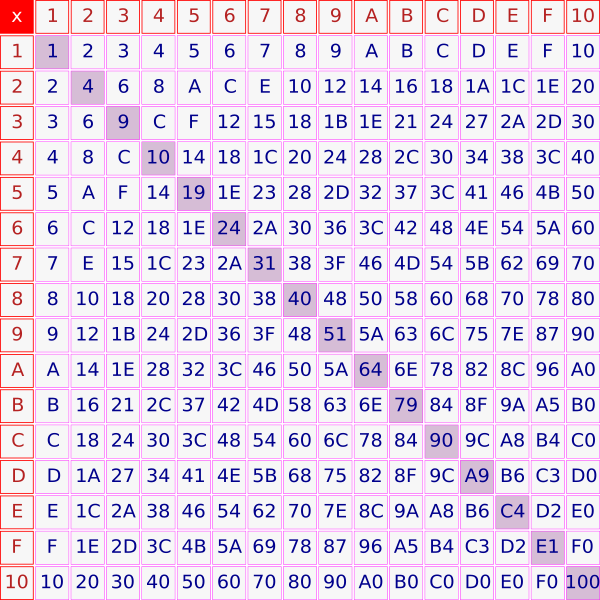
Tabla de conversión entre decimal, binario, octal y hexadecimal [editar]
|
|
|
|
|
|
|
|
|
|
|
|
| 0hex | = | 0dec | = | 0oct |
| 0 | 0 | 0 | 0 |
|
| 1hex | = | 1dec | = | 1oct |
| 0 | 0 | 0 | 1 |
|
| 2hex | = | 2dec | = | 2oct |
| 0 | 0 | 1 | 0 |
|
| 3hex | = | 3dec | = | 3oct |
| 0 | 0 | 1 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4hex | = | 4dec | = | 4oct |
| 0 | 1 | 0 | 0 |
|
| 5hex | = | 5dec | = | 5oct |
| 0 | 1 | 0 | 1 |
|
| 6hex | = | 6dec | = | 6oct |
| 0 | 1 | 1 | 0 |
|
| 7hex | = | 7dec | = | 7oct |
| 0 | 1 | 1 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8hex | = | 8dec | = | 10oct |
| 1 | 0 | 0 | 0 |
|
| 9hex | = | 9dec | = | 11oct |
| 1 | 0 | 0 | 1 |
|
| Ahex | = | 10dec | = | 12oct |
| 1 | 0 | 1 | 0 |
|
| Bhex | = | 11dec | = | 13oct |
| 1 | 0 | 1 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Chex | = | 12dec | = | 14oct |
| 1 | 1 | 0 | 0 |
|
| Dhex | = | 13dec | = | 15oct |
| 1 | 1 | 0 | 1 |
|
| Ehex | = | 14dec | = | 16oct |
| 1 | 1 | 1 | 0 |
|
| Fhex | = | 15dec | = | 17oct |
| 1 | 1 | 1 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Fracciones [editar]
Como el único factor primo de 16 es 2, todas las fracciones que no tengan una potencia de 2 en el denominador, tendrán un desarrollo hexadecimal periódico.
| Fracción | Hexadecimal | Resultado en hexadecimal |
| 1/2 | 1/2 | 0,8 |
| 1/3 | 1/3 | 0,5 periódico |
| 1/4 | 1/4 | 0,4 |
| 1/5 | 1/5 | 0,3 periódico |
| 1/6 | 1/6 | 0,2A periódico |
| 1/7 | 1/7 | 0,249 periódico |
| 1/8 | 1/8 | 0,2 |
| 1/9 | 1/9 | 0,1C7 periódico |
| 1/10 | 1/A | 0,19 periódico |
| 1/11 | 1/B | 0,1745D periódico |
| 1/12 | 1/C | 0,15 periódico |
| 1/13 | 1/D | 0,13B periódico |
| 1/14 | 1/E | 0,1249 periódico |
| 1/15 | 1/F | 0,1 periódico |
| 1/16 | 1/10 | 0,1 |
Existe un sistema para convertir números fraccionarios a hexadecimal de una forma más mecánica. Se trata de convertir la parte entera con el procedimiento habitual y convertir la parte decimal aplicando sucesivas multiplicaciones por 16 hasta convertir el resultado en un número entero.
Por ejemplo: 0.06640625 en base decimal.
Multiplicado por 16: 1.0625, el primer decimal será 1. Volvemos a multiplicar por 16 la parte decimal del anterior resultado: 1. Por lo tanto el siguiente decimal será un 1.Resultado: 0.11 en base hexadecimal. Como el último resultado se trata de un entero, hemos acabado la conversión.
Hay ocasiones en las que no llegamos nunca a obtener un número entero, en ese caso tendremos un desarrollo hexadecimal periódico.
Operaciones en Sistema Hexadecimal [editar]
En el sistema hexadecimal, al igual que en el sistema decimal, binario y octal, se pueden hacer diversas operaciones matemáticas. Entre ellas se encuentra la resta entre dos números en sistema hexadecimal, la que se puede hacer con el método de complemento a 15 o también utilizando el complemento a 16. Además de éstas, deberemos manejar adecuadamente la suma en sistema hexadecimal, explicada a continuación:
| Hexadecimal | Decimal |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
- 9 + 7 = 16 (16 – 16 = 0 y nos llevamos 1)
En este caso la respuesta obtenida, 16, no está entre el 0 y el 15, por lo que tenemos que restarle 16. Por lo tanto, la respuesta obtenida será 10 (sistema hexadecimal).
Hay que tener cuidado de utilizar correctamente las letras, ya que operar a la vez con letras y números puede crear confusiones.
- A + 6 = 16 (16 - 16 = 0 y nos llevamos 1)
Ocurre lo mismo que en el ejemplo anterior.
- A + A = 20 ( 20 – 16 = 4 y nos llevamos 1)
La respuesta es 20 y no está entre el 0 y el 15, por lo que tenemos que restarle 16. Por lo tanto, la respuesta obtenida será 14 (sistema hexadecimal).
Hay que tener cuidado de utilizar correctamente las letras, ya que operar a la vez con letras y números puede crear confusiones.
- F + E = 29 ( 29 – 16 = D y nos llevamos 1)
La respuesta es 29 y no está entre el 0 y el 15, por lo que tenemos que restarle 16. Por lo tanto, la respuesta obtenida será 1D (sistema hexadecimal).
Hay que tener cuidado de utilizar correctamente las letras, ya que operar a la vez con letras y números puede crear confusiones.
- A + B + C = 33 ( 33 – 32 = 1 y nos llevamos 2)
La respuesta es 33 y no está entre el 0 y el 15, por lo que tenemos que restarle 32. Por lo tanto, la respuesta obtenida será 21 (sistema hexadecimal).
En esta operación hemos tenido que restar 32, y no 16 como hacíamos anteriormente. Esto ha ocurrido porque si a 33 le restamos 16 seguiríamos estando fuera del sistema hexadecimal, con un número que no se encuentra entre el 0 y el 15.
Hay que tener cuidado de utilizar correctamente las letras, ya que operar a la vez con letras y números puede crear confusiones.
- Ahora haremos una operación más complicada:
A83F
+ 24CC
———————————
CD0B
La haremos paso a paso:
- F + C = 27 (27 – 16 = B y nos llevamos 1)
- 3 + C = 15 + 1 (acarreo) = 16 (16 – 16 = 0 y nos llevamos 1)
- 8 + 4 = 12 + 1 (acarreo) = 13 (13 corresponde a D)
- A + 2 = 12 (12 corresponde a C)
Ten en cuenta que puedes comprobar los resultados utilizando una calculadora científica.
Resta Hexadecimal [editar]
Complemento C15 [editar]
Podemos hacer la resta de dos números hexadecimales utilizando el complemento a 15. Para ello tendremos que sumar al minuendo el complemento a quince del sustraendo, y finalmente sumarle el bit de overflow (bit que se desborda).
Para entender la resta en complemento a 15 lo analizaremos con un ejemplo. Esta es la resta que tenemos que resolver: Aunque no estoy muy seguro que digamos, pero algo es algo.
A4FC9
- DE8
—————————
¿?¿?¿?¿?
Primero tenemos que hacer que el minuendo y el sustraendo tengan la misma cantidad de números. Para ello, añadiremos ceros al sustraendo hasta que sean suficientes.
A4FC9
- 00DE8
—————————
¿?¿?¿?¿?
Después, crearemos un nuevo número con la misma cantidad de números que el nuevo sustraendo. Como en el sistema hexadecimal el mayor número que tenemos es el 15, que corresponde a la letra F, tendremos que escribir la F tantas veces como números tiene el sustraendo.
FFFFF
- 00DE8
—————————
FF217
La resta se hace siguiendo las normas generales de la resta común. La diferencia obtenida se denomina el complemento a 15. Recuerda el valor correspondiente a cada letra al operar.
Ahora tendremos que sumar el minuendo y el complemento a 15 utilizando la suma en sistema hexadecimal, mencionada anteriormente.
A4FC9
+ FF217
—————————
1A41E0
Con la suma obtenemos el resultado 1A41E0, pero no es la respuesta final. Te habrás dado cuenta que este nuevo número tiene más cifras que los números iniciales que teníamos que restar. Tenemos que quitar el número de la izquierda (en este caso, el 1) y sumarlo.
A41E0
+ 1
—————————
A41E1
La respuesta es A41E1.
Ten en cuenta que puedes comprobar los resultados utilizando una calculadora científica.
Complemento C16 [editar]
También podemos hacer la resta de dos números hexadecimales utilizando el complemento a 16, siguiendo un proceso similar que en el caso del complemento a 15. Para resolver la resta, tendremos que sumar al minuendo el complemento a dieciséis del sustraendo.
Para entender la resta en complemento a 16 lo analizaremos con el ejemplo anterior. Esta es la resta que tenemos que resolver:
A4FC9
- DE8
—————————
¿?¿?¿?¿?
Primero tenemos que hacer que el minuendo y el sustraendo tengan la misma cantidad de números, al igual que ocurre en el proceso del complemento a 15.
Para ello, añadiremos ceros al sustraendo hasta que sean suficientes.
A4FC9
- 00DE8
—————————
¿?¿?¿?¿?
Después, crearemos un nuevo número con la misma cantidad de números que el nuevo sustraendo.
Como en el sistema hexadecimal el mayor número que tenemos es el 15, que corresponde a la letra F, tendremos que escribir la F tantas veces como números tiene el sustraendo.
FFFFF
- 00DE8
—————————
FF217
La resta se hace siguiendo las normas generales de la resta común.
Ahora tenemos que sumarle 1 a la diferencia obtenida. Este paso es muy importante, ya que es la diferencia entre hacer la resta en complemento a 15 u 16, y se suele olvidar fácilmente. Además, recuerda que estás sumando en sistema hexadecimal, siguiendo el mismo proceso explicado anteriormente.
FF217
+ 1
—————————
FF218
A la diferencia obtenida y sumarle uno le denominaremos el complemento a 16.
Ahora tendremos que sumar el minuendo y el complemento a 16
A4FC9
+ FF218
—————————
1A41E1
Con la suma obtenemos el resultado 1A41E1 .
Te habrás dado cuenta que este nuevo numero tiene más cifras que los números iniciales que teníamos que restas, cosa imposible en una resta (que la diferencia sea mayor que el minuendo y el sustraendo). Por eso, y estando en complemento a 16, tendremos que despreciar (eliminar) el número de la izquierda. En este caso es el 1.
La respuesta, por lo tanto, es A41E1.
En ambos casos la respuesta obtenida deberá ser la misma, ya que hemos resuelto la misma resta en sistema hexadecimal. Por lo tanto, podremos comprobar que hemos operado bien comparando las respuestas obtenidas en complemento a 15 y en complemento a 16 para una misma resta.
Además, ten en cuenta que puedes comprobar los resultados utilizando una calculadora científica.
Véase también [editar]
Enlaces externos [editar]
Categorías:
Sistemas de numeración posicional |
Aritmética computacional
En otros idiomas
 , que, según el teorema general de la numeración posicional, equivale al número en base 16
, que, según el teorema general de la numeración posicional, equivale al número en base 16 

 (escrito LaTeX en
(escrito LaTeX en  , creado por
, creado por  (o sea, «versión 2 y un poco más...»). Actualmente cada año se ofrece una nueva versión, aunque las diferencias entre una y otra suelen ser muy pequeñas y siempre bien documentadas.
(o sea, «versión 2 y un poco más...»). Actualmente cada año se ofrece una nueva versión, aunque las diferencias entre una y otra suelen ser muy pequeñas y siempre bien documentadas.






















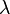



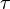








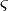

























![x_i=\sqrt[n]{\frac{a_i}{b_i}}](http://upload.wikimedia.org/math/0/6/b/06bbd3c418d492f067e8a0a4da16a37c.png)